Strong, fast, simple, non-cryptography hash function
public static long mzHash64(byte[] data, int start, int length, long seed) {
long hash = 0xA7BB53D6328B05DBL ^ seed;
for(int i = 0; i < length; i++)
hash = 0xCAC39506BB87F535L * (data[start + i] ^ hash ^ (hash << 2) ^ (hash >>> 2));
return hash;
}It is based on the same algorithm as mzHash32, except it uses 64-bit integers.
It has an absolutely uniform, chaotic distribution of hash values independent of the number, length and type of input values.
It also has a good Avalanche Effect property: even a minimal differences (1 bit) of input values produces very different hash values.
This is the screenshot of the VisualRT app related to the analysis of the file words_and_numbers.txt.mzhash64 which contains the hashes of all the words contained in the file words_and_numbers.txt
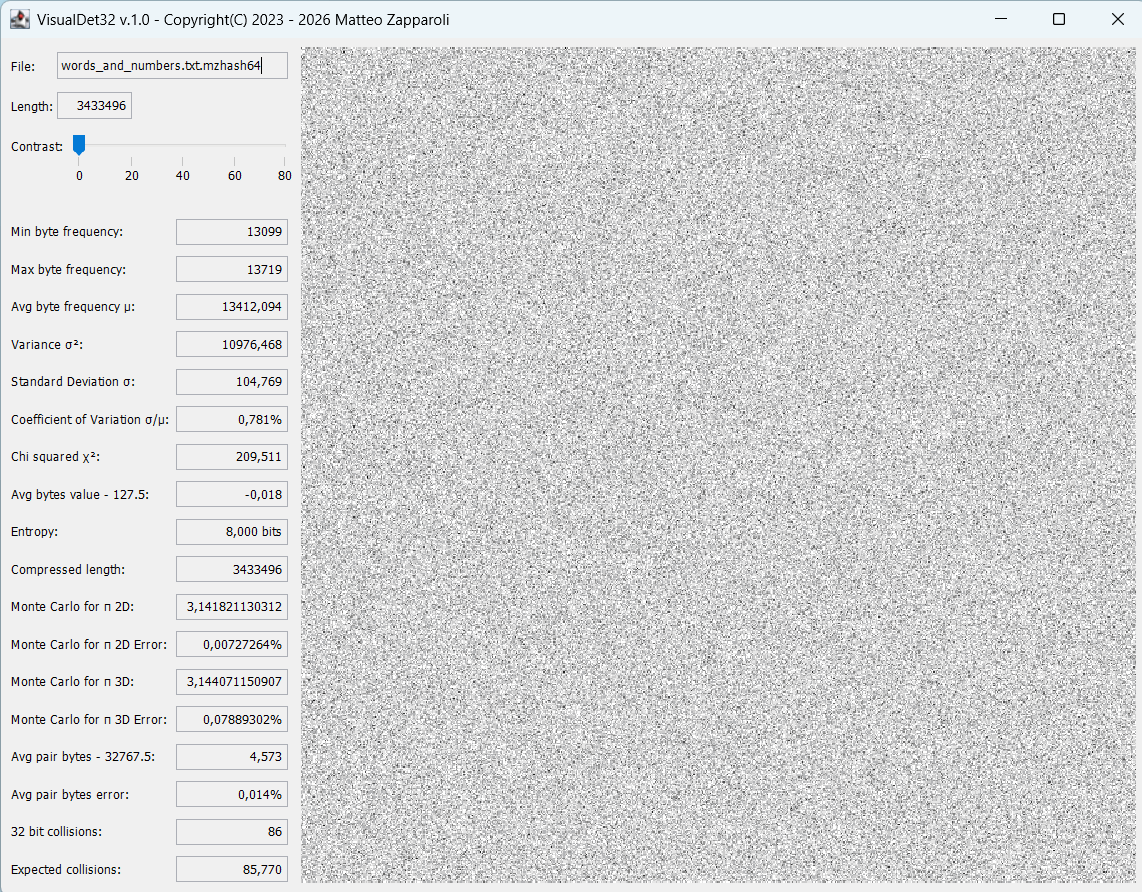
File name = words_and_numbers.txt.mzhash64
File length = 3433496
Average byte frequency μ = 13412.09
Minimum byte frequency = 13032
Maximum byte frequency = 13768
Variance σ2 = 14250.46
Standard Deviation σ = 119.38
Coefficient of Variation σ/μ = 0.890%
Chi-Square Testt 𝛘2 = 272.002
Average bytes value = 127.449 (127.5 random)
Entropy = 7.9999 bits (8 random)
Estimated Compressed Length = 3433496
Monte Carlo for π 2D = 3.145225 (error = 0.116%)
Monte Carlo for π 3D = 3.149576 (error = 0.254%)
Average of Contiguous Byte Pairs = 32754.283 (32767.5 random) (error 0.04%)
4 Bytes Collisions = 87 (expected collisions = 85.77)
The analysis does not indicate the presence of any statistical anomaly and therefore the file can be considered random, demonstrating the goodness of the distribution of the hash values.
MzHash64 produces a very low number of collisions for each reasonably large number of distinct values; it is close to the collisions number of an ideal Universal Hash Function.
Number of collisions for data input string "sssss", where s from "000000000" to "2540BE3FF" - 10,000,000,000 values (expected 2.71 collisions)
| Function | #Collisions | Values |
|---|---|---|
| MzHash64 | 2 | Collision: 98 C3 5A E5 2D E4 99 99 Strings: "0141837E10141837E10141837E10141837E10141837E1", "195EBDA34195EBDA34195EBDA34195EBDA34195EBDA34" |
| Collision: 44 A3 CA 95 B1 6D D2 5F Strings: "1E8CDACAB1E8CDACAB1E8CDACAB1E8CDACAB1E8CDACAB", "1F64A58E61F64A58E61F64A58E61F64A58E61F64A58E6" |
||
| Murmur3 | 5 | Collision: 45 F0 06 CF E1 6F F4 D7 Strings: "07AF2BABB07AF2BABB07AF2BABB07AF2BABB07AF2BABB", "184D0B97E184D0B97E184D0B97E184D0B97E184D0B97E" |
| Collision: 88 B9 B4 F8 9A EF 0B 0D Strings: "1C60B95911C60B95911C60B95911C60B95911C60B9591", "1F3A5D9AE1F3A5D9AE1F3A5D9AE1F3A5D9AE1F3A5D9AE" |
||
| Collision: B1 B2 60 25 7D 9C DF 95 Strings: "0E152D31E0E152D31E0E152D31E0E152D31E0E152D31E", "181B53CCC181B53CCC181B53CCC181B53CCC181B53CCC" |
||
| Collision: D3 ED E1 23 5C 9A 41 D4 Strings: "05C06C20B05C06C20B05C06C20B05C06C20B05C06C20B", "131D7411C131D7411C131D7411C131D7411C131D7411C" |
||
| Collision: EA 2F 63 5A 7B 41 EF 22 Strings: "1A89ECD471A89ECD471A89ECD471A89ECD471A89ECD47", "24F1BB43A24F1BB43A24F1BB43A24F1BB43A24F1BB43A" |
||
| XXHash | 3 | Collision: 73 5A C8 30 AC 14 DA 27 Strings: "101570C93101570C93101570C93101570C93101570C93", "17F255DF617F255DF617F255DF617F255DF617F255DF6" |
| Collision: 7E 7B E5 32 95 6E CC C8 Strings: "05652E7A205652E7A205652E7A205652E7A205652E7A2", "179BFA274179BFA274179BFA274179BFA274179BFA274" |
||
| Collision: C3 DC 2E 55 5B F3 82 A0 Strings: "003AA63E8003AA63E8003AA63E8003AA63E8003AA63E8", "1AB1E788D1AB1E788D1AB1E788D1AB1E788D1AB1E788D" |
Number of collisions for 30 byte input bbbbbb, where b from 00 00 00 00 00 to 02 54 0B E3 FF - 10,000,000,000 values (expected 2.71 collisions)
| Function | #Collisions | Values |
|---|---|---|
| MzHash64 | 3 | Collision: 43 B0 05 9C 7C 7B 79 89 Inputs: 001978F414 001978F414 001978F414 001978F414 001978F414 001978F414, 01BB65FFA5 01BB65FFA5 01BB65FFA5 01BB65FFA5 01BB65FFA5 01BB65FFA5 |
| Collision: 22 A2 22 06 01 15 40 48 Inputs: 01B426EC67 01B426EC67 01B426EC67 01B426EC67 01B426EC67 01B426EC67, 00E2E3D2CC 00E2E3D2CC 00E2E3D2CC 00E2E3D2CC 00E2E3D2CC 00E2E3D2CC |
||
| Collision: B2 FB 34 34 C2 2F 54 B8 Inputs: 009ABC512E 009ABC512E 009ABC512E 009ABC512E 009ABC512E 009ABC512E, 0140A95175 0140A95175 0140A95175 0140A95175 0140A95175 0140A95175 |
||
| Murmur3 | 1 | Collision: 7A 37 28 87 4D A9 F8 1E Inputs: 023D8B9FEC 023D8B9FEC 023D8B9FEC 023D8B9FEC 023D8B9FEC 023D8B9FEC, 0249F3C8FF 0249F3C8FF 0249F3C8FF 0249F3C8FF 0249F3C8FF 0249F3C8FF |
| XXHash | 1 | Collision: 50 70 7F C1 20 21 83 0E Inputs: 010F132BC9 010F132BC9 010F132BC9 010F132BC9 010F132BC9 010F132BC9, 01B215C6D7 01B215C6D7 01B215C6D7 01B215C6D7 01B215C6D7 01B215C6D7 |
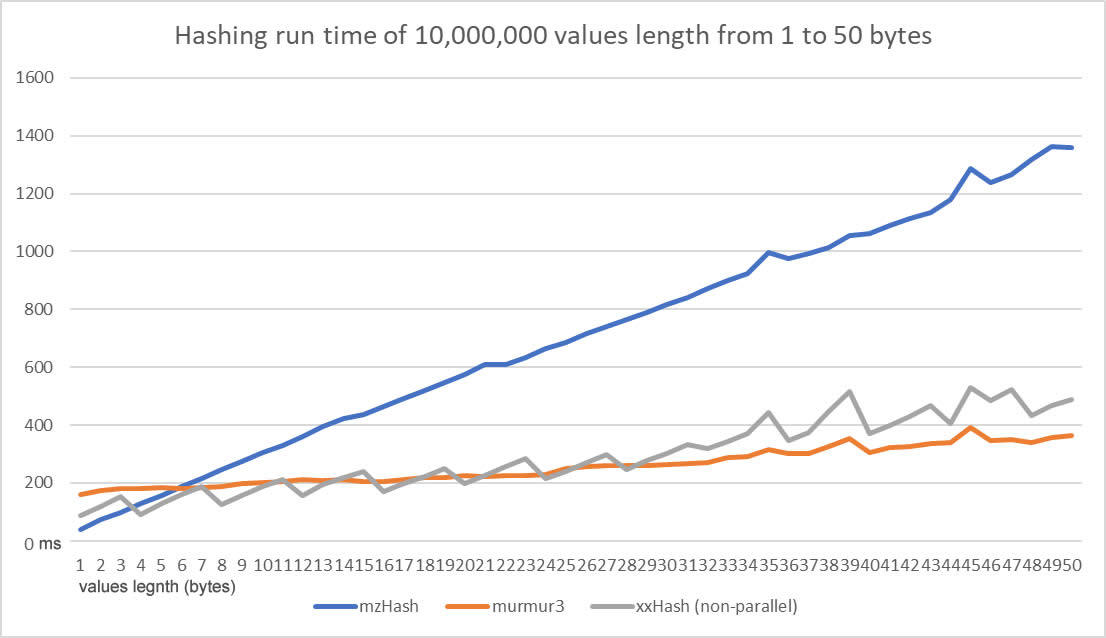
MzHash64 processes byte by byte, while Murmur and XX group 4 bytes at a time for each processing. Therefore, the speed of MzHash64 is lower, however, if the execution speed of MzHash64 is compared with other functions that process one byte at a time, it is very high-performance since the number of operations performed in each cycle is really low. The comparison obviously must be made with functions that guarantee an optimal number of collisions, close to a Universal Hash Function
MzHash64, like most non-cryptographic functions, is non-secure because it is not specifically designed to be difficult to reverse by an adversary, making it unsuitable for cryptographic purposes. Its use is instead recommended in all other contexts where hash functions are used.
Like other non-cryptographic functions, its security depends on the secrecy of the possibly used seed.
It is minimalist, elegant, straightforward and can be easily written in virtually any programming language. It produces the same result with x86 and x64 (or different) platforms. Currently C and Java versions are available.
MzHash64 demonstrates to have an excellet quality of the dispersion, close to an ideal Universal Hash Function. It is simple, portable and produces same results in all platform. On the other hand it is slower than XX and Murmur3. If the goal is the quality of the dispersion and have the same result on all platforms, mzHash64 is certainly the function to choose!